Converting Mathematica Expressions to C
with Common Subexpression Elimination
I frequently use Mathematica to rearrange or solve symbolic equations to use in C++ programs. While Mathematica is quite powerful for that, it has no facility to hoist common subexpressions into variables. This code does that.
Example to convert
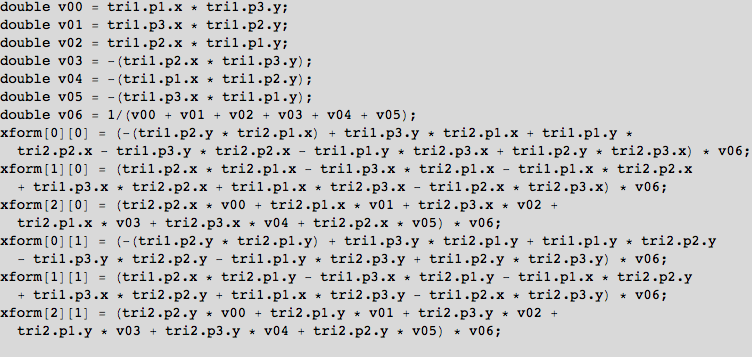
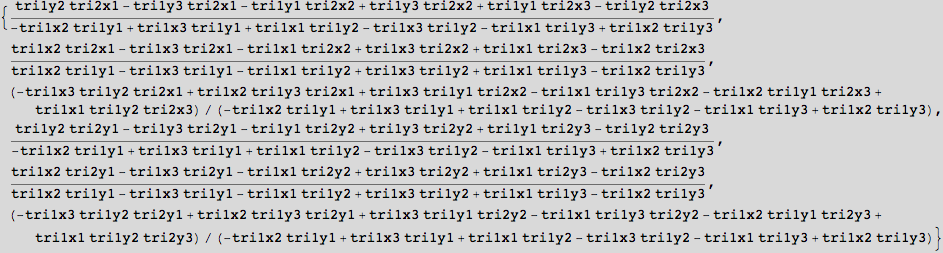
This calculates a closed-form symbolic solution to the problem of finding the affine transform that would turn triangle1 into triangle2. The details are relatively unimportant, but the symbolicSolution output is clearly unusable directly in C. We want to hoist out all the common parts as separate calculations, saving the values in variables.
Creates the matrices and triangles

Solves for the affine transform. This variable is used below as test data
![]()
Conversion code
This code does the conversion. While I haven't tested it on many problems, it seems likely to be generally useful.
Returns a list of all the non-atomic subexpressions in the original expression. The list is sorted so that smaller subexpressions come first, producing a bottom-up search and replacement of the common subexpressions
![]()
The workhorse function. For each subexpression, if the rest of the subexpressions contain instances of the subexpression, accumulate a rule replacing the subexpression with a variable name (symbol). Note that for clarity, no effort is made to avoid symbols with existing values. The result is a list of the original expression with variables substituted for the common parts, and a list of the replacement rules.

The result can have unnecessary variables, used in only one place, so this function removes them by replacing single-use variables by their definitions.

After folding, rename variables so that they're sequentially numbered. Just for prettyness. Note that these variables use a different prefix to avoid mapping collisions. As before, be sure that no variables named v00, etc. have values.
![]()
Combining the above into a single function
![]()
Evaluating the result
This is a computation cost function. I've WAG'd the addition, multiplication, and division (power) costs.

Mathematica has a bunch of built-in symbolic restructuring functions. Here we try most of them to see which one produces the result with the least computation cost.
![]()
![]()
Factor, Together, and Cancel all produce the lowest cost
Compare to the original, unhoisted expression. We've achieved better than a 2x (WAG'd) reduction. Of course, a decent compiler may do just as good, but this will be more readable and manipulable as C source
![]()
![]()
Apply to our test data to get the compressed expression
![]()

Output to C
These functions pick apart the compressed expression and rewrite it as C. This is specific to my original problem, so for other uses, changes will need to be made here

The final output, to be copy/pasted into the C file and tweaked as needed. Note that CForm is somewhat verbose about negations. I have not felt the need to rewrite CForm to fix that.
![]()