2D Matrix Decomposition
This demonstrates the polar decomposition of 2D matrices into their angle, scale, and shear components. The polarDecomp algorithm is taken from Shoemake & Duff "Matrix Animation and Polar Decomposition", 1992.
I found that the formula for the polar decomposition, on page 3, produces rotation matrices that don't account for diagonal axis flipping (swapping x with y). The article seems to factor out the flipping, but I didn't want to have a fourth component. Removing the sign(det(M)) factor eliminated this problem by incorporating the flipping into the rotation matrix.
It's very desirable to decompose a matrix generated by {angle, scale, shear} back into the same part values, but this happens only when scale is positive and shear is zero. If not, the rotation is affected. At least, the parts are stable once derived from the first matrix. This may help in UI, and certainly in interpolation.
Matrix generators
All the matrix ops are Vec . Mat
Rotation
In[17]:=
![]()
Scaling
In[18]:=
![]()
In[19]:=
![]()
Shear
In[20]:=
![]()
In[21]:=
![]()
A handy pre-defined symbolic matrix
In[22]:=
![]()
Out[22]//MatrixForm=
![]()
Returns Q (the rotation matrix) and S, the stretch matrix
Unlike the version in Shoemake & Duff's polar_decomp paper, this one always returns a normal rotation matrix, and thereby accounts for axis flipping
In[23]:=

Returns the angle of a rotation matrix
In[24]:=
![]()
Returns the {x, y} scale of a stretch matrix
In[25]:=
![]()
Returns the {x, y} shear of a stretch matrix
In[26]:=
![]()
Converts the Q and S matrices into {angle, scale, shear}
In[27]:=
![]()
Composition to produce the parts directly from the original matrix
In[28]:=
![]()
Recreate the original matrix from the parts
In[29]:=
![]()
Testing
This loses precision enough to require the SetPrecision
In[30]:=

Test that matrix decomposition and recomposition is equal to the original
In[31]:=
![]()
In[32]:=
![]()
Out[32]=
![]()
Test that the same components are recovered from matrices generated by random components
Note that they aren't the same unless scale is positive and shear is zero
In[33]:=
![]()
In[34]:=

In[35]:=
![]()
Out[35]=
![]()
Test that components are equal after two passes of decomp/comp. The 1st pass output is "canonical"
This always succeeds, so long as the precision is kept down
In[36]:=
![]()
In[37]:=
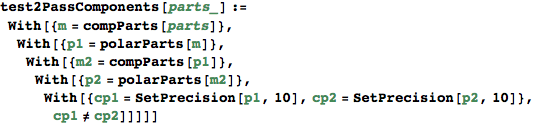
In[38]:=
![]()
Out[38]=
![]()
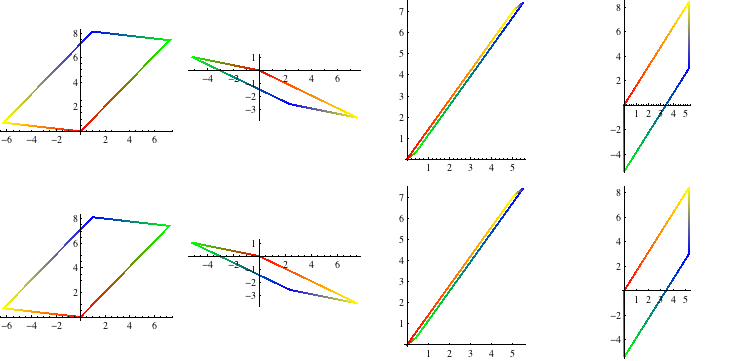
Examples
Note that Geometric transform does M . V, but that doesn't matter so long as it's consistent
Draw a transformed unit square, colored to make it easy to see axis flipping
In[39]:=

Draw some random examples
In[40]:=
![]()
Out[40]=